비전쪽을 잘 모르다보니 Wasserstein GAN이 나왔을 때도 어렵다는 얘기 정도만 듣고 따로 찾아보지는 않았는데 이번에 스토리 생성 관련 연구를 하면서 이 Wasserstein Distance를 활용한 Auto-encoder가 나와서 소개하고자 합니다.
Backgrounds
1. Wasserstein Distance(편의상 W-dist)
W-dist는 두 확률 분포간의 거리를 나타내는 방식으로 Optimal Transport 문제에서 유래했다. 확률 분포를 흙더미라고 생각하고 \(P(X)\)를 \(Q(X)\)로 옮길 때 필요한 일의 양을 두 확률 분포의 거리라고 정의할 수 있다. 고전역학에서 일의 양은 힘 곱하기 거리로 표현되는데, 확률 분포의 무게는 합이 1로 제한되고, 거리는 단순히 euclidean distance로 표현할 수 있을 것이다. 이때 \(P\)의 \(x\)위치에서 \(Q\)의 \(y\)위치로 옮기는 확률 분포의 양을 \(\gamma(x,y)\)로 표현하고, 거리 함수(cost)를 \(c(x,y)\)로 표현해보자. 그러면 W-dist는 아래와 같이 정의할 수 있다.
$$ W(P,Q) = \inf_{\gamma \sim \Gamma[P,Q]} \mathbb{E}_{X,Y \sim \gamma} [c(X,Y)] ,\\ \textrm{where } \int_x \gamma(x,y) dx = Q(Y), \int_y \gamma(x,y) dy = P(X), \gamma(x,y) \geq 0 $$
2. Variational Autoencoder
데이터셋의 Low dimension Latent Variable을 학습하기 위한 모델 중 하나인 VAE는 그 수학적 배경과 단순한 구현으로 인해 여전히 많이 사용되는 기법이다. 단순히 point estimate을 하는 auto encoder와 달리 VAE는 latent variable에 대한 gaussian prior 및 posterior를 가정하여 얻어진 tractable한 ELBO(Evidance Lower Bound)를 최대화 하는 방식으로 posterior 분포를 근사한다. 충분 통계량을 네트워크의 아웃풋으로 가정하는 amortized variational inference, 샘플링을 하면서도 gradient를 계산할 수 있도록 stochasticity를 고립시키는 reparametrization trick 등 이제는 매우 유명해진 기법들을 볼 수 있는 기념비적인 연구이기도 하다.
VAE를 최적화하는 ELBO는 아래와 같이 계산된다.
$$ L_{\textrm{VAE}} = \mathbb{E}_{q_\phi(z|x)} [ \log p_\theta (x|z) ] - D_{\textrm{KL}}(q_\phi(z|x) | p(z)) $$
첫번째 term은 보통 reconstruction loss로 계산하고(Mean Squared Error 등), 뒤의 KL divergence를 해석적으로 표현하기 위해 approximate posterior \(q(z|x)\)에 대해 normal 가정을 하게 되는데 이것이 latent variable의 표현력을 떨어뜨리는 한계가 될 수 있다. 단적으로 자연어를 모델링한다고 했을 때, '잘한다'라는 표현은 '칭찬'의 의미일 수도 있고 '비꼼'의 의미일 수도 있다. latent 공간에 이런 의미가 잘 모델링 되었다고 생각하면 분명 두 개 이상의 local maxima를 갖는 분포가 되어야 할 것이라고 생각할 수 있다. 하지만 VAE는 이것을 unimodal하게 가정해버리므로 suboptimal할 수밖에 없다. 이런 VAE의 근본적인 한계는 KL divergence를 해석적으로 계산하려고 하기 때문에 나온다. 그렇다면 다른 거리 metric을 가정하면 prior 및 posterior에 대한 자유도가 좀 더 높아질 수 있지 않을까?
Waserstein Autoencoder
위에서 정의된 w-dist를 최소화하는 방식으로 Generator \(G_X\)를 만든다고 생각해보자. 우리의 태스크는 이제 \(P_X\)를 따르는 데이터셋 D를 가지고 있을 때, \(G_X\)와 \(P_X\)의 w-dist를 최소화하도록 G_X를 학습하는 일이다. 다행히도 \(\gamma \sim \Gamma[p,q]\)를 찾는 대신, 사후 분포인 \(Q(Z|X)\)만 찾으면 된다는 것이 알려져 있다. (
appendix 참조) 대신 \(Q(Z) = \mathbb{E}_{X\sim P_X} [Q(Z|X)] = P(Z)\)라는 hard constraint가 있다. 즉 아래 식이 성립한다.
$$ \inf_{\gamma \in \Gamma[p,q]} \mathbb{E}_{(x,y) \sim \gamma} [ c(x,y) ] = \inf_{Q : Q_Z = P_Z} \mathbb{E}_{P_X}\mathbb{E}_{Q(Z|X)} [c(X, G(Z))] $$
위의 hard constraint를 lagrange multiplier를 활용해서 soft constraint로 바꾸려면 양수 \(\lambda\)를 곱해서 아래와 같이 표현한다.
$$ D_{\textrm{WAE}}(P_X, P_G) = \inf_{Q(Z|X) \in \mathcal{Q} } \mathbb{E}_{P_X} \mathbb{E}_{Q(Z|X)} [c(X, G(Z))] + \lambda \cdot D_Z (Q_Z, P_Z) $$
위의 식에서 우리는 \(Q(Z|X)\)를 \(\phi\)로 매개화하고 그것을 학습할 것이므로 infimum을 제거한 부분을 loss로 사용할 수 있다. (이 부분도 엄밀한 equality는 아니고 근사값으로 볼 수 있다.) 이 식에서 cost 함수 부분을 L1이나 L2 같은 일반적인 거리로 둔다면 우리가 알고 있는 L1, L2 reconstruction term이 나오는 것을 쉽게 확인할 수 있다.
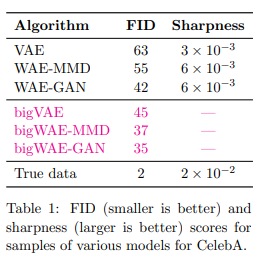
VAE와 달라지는 부분은 결국 regularization term이라는 얘기다. VAE는 모든 Z들의 posterior가 P(Z)와 같아지게 하지만 WAE는 posterior의 mixture( \( = \mathbb{E}_X[ Q(Z | X) ] \) )가 P(Z)와 같아지게 만든다. 따라서 아래 그림처럼 latent code의 표현력을 더 잘 보존할 수 있게 된다.
regularization term으로 prior와 posterior mixture의 거리(\(D\))를 최소화해야 하는데,
여기에서 이 거리라는 개념를 MMD(Maximum Mean Discrepancy)로 정의할 수도 있고, GAN discriminator로 정의할 수도 있다. 그 두 가지 모두 성능은 유사하며 알고리즘은 아래와 같다.
Divergence Modeling
1. WAE-GAN
WAE GAN은 divergence 텀을 prior-posterior discriminator의 negative log likelihood로 봤다고 생각하면 된다. 먼저 prior 분포의 z와 posterior 분포의 z를 구분하는 binary classifier를 만들고 그 classifier에서 prior로 분류할 확률을 divergence로 사용하는 것이다. 아주 직관적인 방식이다. 대신 이 방식은 classifier학습을 위해 AE 학습 외에 별도 backprop을 해줘야 한다.
2. WAE-MMD
MMD(mean maximum discrepancy)는 두 분포 사이의 거리를 나타내는 지표 중 하나로 아래와 같은 정의를 갖는다.
$$ \textrm{MMD}(P,Q) = \| \mathbb{E}_{X \sim P}[\phi(X)] - \mathbb{E}_{Y \sim Q}[\phi(Y)] \|_{\mathcal{H}} $$
여기에서 \( \phi(\cdot)\)는 피쳐 스페이스로 보내는 맵핑 함수라고 생각하면 된다. 간단하게 생각해서 \( \phi(x) = x\) 인 경우에는 MMD는 단순히 두 분포의 평균의 차이가 된다. 만약 \( \phi(x) = (x,x^2)\)이라면 MMD는 \( \sqrt{(\mathbb{E}[X] - \mathbb{E}[Y])^2 + (\mathbb{E}[X^2] - \mathbb{E}[Y^2])^2} \)이 된다. 이 경우 두 분포의 평균과 분산을 모두 반영한 거리라고 볼 수 있다. 이런 관점에서 임의의 \(n\)차 모먼트까지 고려할 수 있다면 더 표현력이 좋아질 것이다. 피쳐 스페이스에서 무한차원을 갖는 맵핑함수를 implicit하게 만들어낼 수 있는 방법이 커널 트릭이다.
위의 MMD의 제곱 값을 구하면 다음과 같다.
저 커널함수를 RBF \( k(x,y) = \exp{(- \frac{\| x-y \|^2}{2 \sigma^2} )} \) 등으로 정의하면 feature space \( \mathcal{H} \)에서의 implicit dimension은 무한대가 된다. (그걸 보는 방법은 단순히 \( \|x-y\| \)를 중심으로 tayler expansion을 해보면 된다.)
다만 gaussian kernel은 tail이 너무 얕아서 heavy tail을 가진 inverse multiquadratic kernel을 사용했다고 한다. 위 알고리즘처럼 샘플을 \(n\)개 뽑았다고 가정하면 kernel trick을 사용한 결과는 첫번째, 두번째 텀에서는 자기 자신과의 유사도를 제외한 \(n(n-1)\)개, joint 분포(마지막 텀)에서는 \(n^2\)개가 나와서 위와 같은 평균식이 나오게 된다.
이 경우 prior나 posterior에 대해서 특정한 분포적 가정을 두지 않기 때문에 샘플링만 가능하다면 더 자유롭게 모델링할 수 있다는 장점이 있다. VAE에서 지겹게 쓰던 isotropic gaussian 가정을 버려도 된다는 것이다! 그래서 위에서 언급했던 Multimodal Prior를 표현하기 위해 Mixture of Gaussian을 사용한
논문들이 나온 것들도 확인할 수 있다. 물론 posterior를 분포로 가져가려면 amortized variational inference를 써야 하기 때문에 충분 통계량을 모델링하기 위해 결국 어떤 분포를 가정 할 수밖에 없긴 하다. 그래도 posterior가 point estimate인 경우에도 학습이 가능하다는 것은 장점이라고 할 수 있다.
3. Summary
formulation은 다르게 시작했지만 Variational Autoencoder와 동일하게 reconstruction term + regularization term으로 구성이 동일하게 되는 것을 볼 수 있고, regularization term을 어떻게 정의하느냐에 따라 두 가지 형태가 나올 수 있다. MMD 같은 경우는 다양한 함수적 가정을 가진 prior를 정의할 수 있어 VAE 보다 자유도가 높다고 할 수 있다.







댓글
댓글 쓰기